■ＡＩによる問題解決
さいきん、囲碁や将棋などの世界で、人工知能（AI、Artificial Intelligence）の力が、一流棋士を圧倒するようになってきている。
碁の世界では、2017年3月23日のワールド碁チャンピオンシップで、井山裕太六冠が、
「Deep Zen Go（ディープ　ゼン　ゴ）」に敗れている。また、同じく2017年の５月には、世界最強の棋士とされる中国の柯潔（かけつ）九段が、グーグル傘下のイギリスのディープマインド社の「アルファ碁」に、三番勝負で三連敗している。惨敗といってよい。
将棋の世界でも、将棋電王戦二番勝負で、2017年の4月1日と5月20日に、佐藤天彦（あまひこ）名人が、「PONANZA（ポナンザ）」に、二番とも、完敗している。
チェスの世界では、すでに、1997年に、当時の世界王者が、ＡＩの「ティーブルー」に敗れている。オセロの世界でも、1997年に、世界王者が、ＡＩの「ロジステロ」に、六戦全敗で敗れている。

私は、「邪馬台国問題」や「日本語の起源問題」、「日本人の起源問題」などの、日本古代史上の大問題なども、確率論や統計学、そしてコンピュータなどの力をかりて、まったく機械的に解決をみる可能性が大きいと考えている。
私は、そのような方向へのこころみとして、邪馬台国問題では、『邪馬台国は、99.9％福岡県にあった』（勉誠出版、2015年刊）を出した。これは、ベイズの統計学によって、邪馬台国が、福岡県にあった確率や、奈良県にあった確率などを計算したものである。東京大学名誉教授の統計学者で、わが国におけるベイズ統計学者（ベイジアン）の第一人者ともいえる松原望氏と、長時間の検討を行なったモデルにもとづく計算である。

日本語の起源問題では、『研究史日本語の起源』（勉誠出版、2009年刊）や、『日本語の誕生』（大修館書店、1990年刊）などを出した。これらは、日本語と、日本の周辺の言語、四十八言語との近さの度合を、基礎語彙などにもとづいて計算したものである。基本的には、フィッシャー流の統計学により、日本語と偶然以上の一致（有意の一致）を示すものは、どのような言語であるかを、計算して、とりだす方法による。大量の計算はコンピュータの利用なしには不可能である。
統計学や確率論、そしてコンピュータの利用などにもとづく情報処理の技術は、すでに、これらの諸問題解決に必要な技術や方法じたいは、提供しているとみられる。

共産中国の建設者、毛沢東は、かつてのべた。
「揚子江は、あるところでは北に流れ、あるところでは南に流れ、あるところでは西にすら流れている。しかし、大きくみると、かならず西から東へ流れている。」
碁でも、将棋でも、局地戦にこだわりすぎると、全体の勝利を失なうことになる。

 

■問題の所在
「ことば」に特別の関心を示す作家、清水義範の作品に，『序文』という小説がある（講談社文庫『蕎麦ときしめん』所収）。
『序文』は、一種のパロディー小説である。学者の文体をかりて、「英語の起源は日本語だ」と主張する。
「name（ネーム）」と「namae（名前）」、「owe（負う）」と「ou（負う）」、「kill （殺す）」と「kiru（斬る）」など、ひとつの新学説をなすのに十分と思われる290例もが発見されたという。
「battle（戦い）」と「batoru（場取る）」、「boy（少年）」と「boｙａ（坊や）」などの例にいたって、ふつうの読者は、この小説は冗談だと思って、笑いだすだろう。
しかし、じつは現在でも、英語をはじめとする印欧語と日本語とが、関係があると主張している何人かの研究者がいる。
たとえば、琉球大学の教授であった城間（しろま）正雄は，『日本民族形成の一視点（日本語と印欧語の関係の考察）』（雄山閣出版、1979）をあらわし、日本語の「火（ひ）」と、英語の「fire」をはじめとする印欧諸言語の「火」を意味する語の形、また、日本語の「新（にひ、にふ）」と、英語の「new」をはじめとする印欧諸言語の「新」を意味する語の形などを、古形にさかのぼり、くわしく考察している。
城間は、たとえば、つぎのように記す。
「『新（にひ）』についてのヨーロッパ諸語と日本語の対応・類似関係は明確である。」

どの言語でも、何万という単語をもつ。いっぽう、人間が発音し、聞き分けられる音は、せいぜい数十種類である。そのため、世界の任意の言語をえらぶとき、偶然、意味と音（形）とが似ている単語を、200～300は、さがしだすことができる。
明治以後の日本語の起源探究論のほとんどは、基本的には、『序文』と同じ方法によっていたといっても、過言ではない。
ここに、『序文』というパロディー小説の深刻さがある。
学者は、みずからがとりあげた２言語が、世界の任意の２言語よりも、とくに関係が密接であることを、「客観的に」証明しなければならない。
たんに、この２言語には、意味と音（形）とが、こんなにも似た、あるいは、対応するようにみえる単語が、こんなにもある、という事例の提示だけでは、不十分である。
探究の方法じたいを、きびしく反省しなければいけない時期にきている。

寺田寅彦の提言
私たちが、自然科学から学んだ最大のものは、「客観性」であろう。
研究者が、「主観的に」問題を「解きえた」と思っただけでは、不十分である。
物理学者であり、随筆家でもあった寺田寅彦は、すでに、1928年に、「比較言語学における統計的研究法の可能性について」（『思想』３月号．岩波文庫『寺田寅彦随筆集』第２巻所収）という随筆を、発表している。そのなかで、寺田は、およそ、つぎのようにのべている。

「……もっとも縁の遠そうな英語でさえ、（日本語と）こじつけようと思えば、かなりにこじつけられない事はない。」
「学者のなかには、２つの国語の間の少数な語彙の近似から、大胆に２つのものの因果関係を帰納しようとする人もあるようであり、また一方では、あまりにも細心で潔癖なため、暗合（偶然の一致、筆者注）の悪戯（いたずら）に欺（あざむ）かれることを恐れて、この種の比較に面迫することを回避する人もあるかもしれない。自分にはこの２つの態度がいつまでもたがいに別に離れて相対しているという事が言語学の進歩に有利であろうとは思わない。むしろ進んで、暗合的なものと因果的なものとを含めた全体のものを取って、なんらかの合理的な篩（ふるい）にかけて偶然的なものと必然的なものとを篩（ふる）いわける事に努力したほうが有利ではあるまいか。そうして、統計的に期待されるべき暗合の確率と、実際の統計的符合率とを対照して、因果関係の『濃度』を示すべき数値を定め、その値の比較的大なるものについて、さらに最初の仮定の再吟味（ぎんみ）を遂行し、その結果にもとづいて修正された新たな仮定を設け、逐次かくのごとくにしていわゆる漸近（ぜんきん）的近似法によって進行すれば、すくなくとも現在よりは、いくらか科学的に研究を進められはしないかと考えるのである。」

いまから９０年近くまえに書かれたとは思えないほど、現代的な文章である。いますこし紹介してみよう。
「統計的方法の長所は、はじめから偶然を認容してかかる点にある。いろいろな『間違い』や『杜撰（ずさん）』でさえも、最後の結果の桁数（ｵｰﾀﾞｰ）には影響しないというところにある。そして、関係要素の数が多くて、それら相互の交渉が複雑であればあるほど、かえってこの方法の妥当性がよくなるという点である。」
「こういうたんねんな吟味をするには、かなりの手数と時間を要する。……（しかし）そのほうの専門の研究者の専門の仕事としてみるときは、他の科学者、たとえば、天文学者、物理学者、化学者などの仕事に比して、それほどめんどうな仕事とは、けっして思われないのである。」
「その昔、独断と畏怖（いふ）とが対峙（たいじ）していた間は、今日の『科学』は存在しなかった。
『自然』を実験室内に捕（とら）えきたったあらゆる稚拙（ちせつ）な『試み』を『実験』の試練にかけて篩いわけるという事、その判断の標準に、『数値』を用いるという事によって、はじめて今日の科学が曙光（しょこう）を現わしたと思われる。もし古来の科学者が、……『試み』にともなう怪我（けが）のチャンスを恐れて、だれも手を下す事をあえてしなかったら、現在のわれわれの自然界に関する知識と利用収穫は、依然として復興期以前の状態で足ぶみしていたであろう。」
「従来とても、統計的のやり方はあるにはあるが、たんに数をかぞえて多いとか少ないとかいうだけでは、なんらほんとうの統計としての意味がないという事である。全体に対する実際の符合率が、偶然による符合率に対する比のみが意味をもつ。」

確率論にもとづく統計学の発展や、コンピュータの普及は、寺田寅彦の発想を、ようやく現実のものとしている。

以上の「問題の所在」「寺田寅彦の提言」は拙著『言語の科学』（朝倉書店、1995年刊）による。

 

■インチキ問答
インチキ問答
私は、以前大学に勤めていたとき、統計学、数学も教えていたことがあった。二百人ぐらいの学生の、統計学の授業のさい、つぎのような質問をしたことがあった。
「こんな話があります。織田信長が桶狭間の戦いのときに、戦いのまえに、軍勢を熱田神宮の境内（けいだい）に集め、戦勝祈願をしました。そのとき、織田信長がいった。
『本日の戦いの吉凶をうらなおう。いま、一文銭を投げさせる。表（おもて）が多く出れば勝利ぞ。』
織田信長は、そういって、小姓に、用意した一文銭を十個投げさせた。すると、十個とも全部表（おもて）がでた。一同、どっと喜び、本日の勝利うたがいなし、と、鯨波（とき）の声をあげて出陣した。しかし、じつは、あらかじめ一文銭の裹を、ヤスリでけずり、裏同士をはりあわせ、表（おもて）しか出ないようにしてありました。

そこで、質問です。
いま、ある人が、十円玉を十回なげて十回とも表をだしてみせるといって、ほんとうに十回つづけて表をだしてみせたとします。そこには、なにか、インチキがあると思う人は、手をあげて下さい。」
すると、七割ぐらいの学生が手をあげた。三割ぐらいの学生は、インチキはないと考えたのである。
「では、インチキはないと思う人の中で、二〇回つづけて表をだしても、インチキはないと思う人、手をあげて下さい。」
すると、二〇人ていどの人が手をあげた。
「では、百回つづけて表をだしても、インチキはないと思う大、手をあげて下さい。」
十人ほどの学生が手をあげた。
このように、順に回数をふやして、手をあげさせた。すると、驚くなかれ、回数を、一万回にふやそうが、十万回にふやそうが、百万回にふやそうが、手をあげつづける学生が三人ほどいた。

私は、たずねた。
「どうして、インチキがないと思うのですか。」
学生が答えた。
「偶然で百万回表がでることだって、ありうると思います。」
私は、今度は、逆に、十回つづけて表をだせば、「インチキがあると思う」と答えた学生に質問した。
「九回つづけて表をだしたばあいはどうですか。」
「八回ではどうですか。」
以下、順に回数をへらしていくと、「三回つづけて表をだしたばあいに、インチキがあると思う人」のところで、手をあげる人は零となった。

推計学が、昔の統計学と異なるもっとも大きな特徴は、この十円玉のような問題に対して、確率の考え方にもとづき、判断を客観的に行なう論理と基準を提供したことである。
推計学では、このようなばあい、つぎのような仮説（帰無仮説という）をもうける。
「仮説　この十円玉の投げ方には、インチキなしかけはないと考える。」
そして、この仮説のもとで、たとえば、十円玉が、十回つづけて表をだす確率を計算するのである。そして、計算した確率が、一定の値よりも小さければ、もとの仮説を、捨てる約束にするのである。一定の値としては、ふつう、「5/100」か、「1/100」をとる。

じっさいに計算してみると、インチキはないという仮説のもとで、十円玉が十回つづけて表をだす確率は、1/1024（＝1/2↑10）となる。この値は、「5/100」「1/100」のいずれよりも小さい。
したがって、もとの「インチキなしかけはない」という仮説はすてられ、「インチキがある」という判断をうけいれることになる。

「インチキなしかけはない」という仮説のもとで、十円玉が百万回つづけて表をだす確率は十の下に、零が三〇万個つく数分（かずぶん）の一よりも小さい。もし、そのようなばあいも、「インチキはない」と判断することにするなら、私たちは、日常においても、学問上においても、なんらの判断もできなくなるはずである。私たちは、日常においても、学問上においても、たえず、より可能性の小さい仮説はすて、より可能性の大きい仮説を、採択して行こうとしているはずである。
私たちは、日常生活においても、「十中八九」正しいと思われる仮説は採択している。いま、あなたがこの本を読まれているときに、突然地震がおきて、天井が落ちてくる「可能性」も、ないわけではない。しかし、そのような「可能性」は、きわめて小さいので、安心して、拙文をお読み下さっているのである。

■コラム　確率
確率は、確からしさの度合いである。０（ゼロ）から、１までのあいだの値をとる。確率0.6を、「60パーセントの確率で」などのように表現することもある。
一枚の十円玉を投げるとき、表のでる確からしさと、裏のでる確からしさとが、同じと考えられるとしよう。このとき、表のでる確率は、二つに一つという意味で、「1/2」と表現される。このばあいは、裏のでる確率も、「1/2」である。
おなじように、サイコロを投げるばあいならば、一の目のでる確率は、六つのうちひとつであるから、「1/6」と表現できる。
じっさいに、十円玉を百回なげて、52回表がでて、48回裏がでたとする。このばあい、じっさいの頻度にもとづいて、表のでる確率は「0.52」と考えることもある。
いま、表のでる確率が「1/2」、裏のでる確率が「1/2」の十円玉があるとする。
この十円玉を二回投げたとき、二回とも表がでる確率を求めてみよう。
このばあい、下の表のように、「１回目が表で、２回目も表」「１回目が表で、２回目が裏」「１回目が裏で、２回目が表」「１回目も２回目も裏」の四とおりの「ばあい」が考えられる。
１回目表、表、裏、裏、
２回目表、裏、表、裏、
二回とも表がでるのは、四つの「ばあい」のうちの一つがおきることになる。よって、二回とも表がでる確率は1/4である。
ところで、この1/4は、「１回目に表のでる確率1/2」と、「２回目に表のでる確率1/2」とをかけあわせた値になっている（1/2×1/2＝1/4）
いろいろな確率は、しばしばこのような掛け算を行なうことによって求めることができる。
確率を用い、この種の演算約束によって、計算を行なうことにより、種々の推測や判断を行なうことができる。

■シフト法
二つの言語の単語の一致の度合いが、偶然で期待される以上のものかどうかを、統計的にしらべる諸方法のなかでは、カリフォルニア大学教授だった言語学者オズワルド（Oswalt,Robert L.1923～2007 アメリカ出身）によってとなえられたシフト法（shift test method）が、考え方が簡明であり、かつ、実際の処理が容易である。しかも、二つの言語のあいだの偶然で期待される以上の一致を、きわめてシャープにとりだしうる長所かある。

オズワルドの方法は、1970年の「文学と言語行動のコンピュータ研究（computer Studies in the Humanities and Verbal Behavior）」誌に発表された論文「遠い言語関係をさぐる（The detection of remote linguistic relationship）」にのべられている。「シフト法」は、コンピュータの利用と密接にむすびついている。
いま、たとえば、日本語と朝鮮語とを、次ページに示す基礎語彙表のような、二百項目の「単語のセット」によって比較するばあいを考えてみよう。

日本語の二百の単語を、W1,W2,W3,･････,W200とし、意味のうえで、できるだけ正確にそれに対応する朝鮮語の二百の単語を、V1,V2,V3,･････,V200とする。
まずW1とV1’W2とV2’･････’W200とV200とをそれぞれ比較し、その二百個のくみあわせのなかで、たとえば、第１番目の子音がいくつ一致しているかをしらべる。

つぎに、ひとつずつずらし、W1とV2’W2とV3’W3とV4’･････,W200とV1とをそれぞれ比較し、その二百個のくみあわせのなかでの語頭の音の一致数をしらべる。これは、ひとつの偶然による一致度を教えてくれる（図参照）。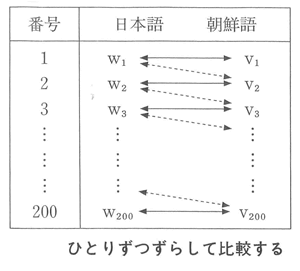

そしてつぎに、いまひとつずらし、W1とV3’W2とV4’W3とV5’･････,W200とV2とをそれぞれ比較し、その二百個のくみあわせのなかでの語頭の音の一致数をしらべる。これも、またひとつの偶然による一致度を教えてくれる。

以下、同様のことを、W1とV200’W2とV1’W3とV2’･････,W200とV199までくりかえす。

このようにくりかえすならば、全部で二百個の一致度がえられる。この二百個の一致度についての度数分布表をつくる。

そして、もし意味が対応するW1とV1’W2とV2’･････’W200とV200とを比較したときの一致数（この値を粗点gross scoreとよび、x0であらわす）が、他の百九十九個の偶然による一致数（この値を、背景点background scoresとよび、ｘであらわす）にくらべ、ずっと大きければ、日本語と朝鮮語との一致数は、偶然によるものではないと考えられる。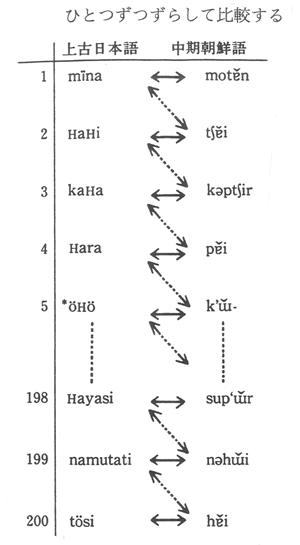

■上古日本語（基本的に奈良時代の日本語）と中期朝鮮語（１５世紀ごろの朝鮮語）とを200語の基礎語彙で一つずつずらして比較すると右図のようになる。
皆（みな）、灰（はい）、皮（かわ）のように比較するのである。
そして、語頭音は変化しにくいため語頭音を比べる。

注：
・中期朝鮮語：
中期朝鮮語は、東京外国語大学の梅田教授の論文「朝鮮語諸方言の基礎語彙統計学的研究」（1963年『朝鮮学報』27）および南広祐編『古語辞典』（東亜出版社刊、ソウル）によった。作成した基礎語彙表は、梅田博之教授にみていただいた。ただし、ハングル（朝鮮の国字）からの転写法は、私たちなりの方法にしたがった（コンピュータにいれるつごうも、若干考慮した）。日本語は、『古事記』『万葉集』の成立した８世紀ごろまでさかのぼれるが、朝鮮語は、ハングルの発明された15世紀中ごろの、中期朝鮮語までしかのぼれない。

・上古日本語、日本語東京方言、首里方言：
上古日本語は、服部四郎氏の『言語学の方法』にのせられているもの（大野晋氏記入）を参考とし、久松潜一監修『新潮国語辞典』（新潮社刊）、上代語辞典編集委員会編『時代別国語大辞典上代編』（三省堂刊）によって作製した。
「上古日本語」は、奈良時代の日本語をさすが、一部平安時代までしかさかのぼれない語がはいっている。＊印のついたものは推定形。母音の甲類、乙類の別などを推定したもの。
「東京方言」も、服部四郎氏が、『言語学の方法』の中で示しておられる基礎語彙表の形に、ほぼしたがった。ただし、あきらかな借用語は、のぞくようにした。たとえば、服部氏は、英語の「husband」にあたる「東京方言」を、「sjuzin（主人）」としておられるが、これを、私は、「'otto（夫）」とした。これは，服部氏と私とで、基礎語彙表作成の目的が異なるからである。服部氏は、２つの言語が分裂した年代を推定する言語年代学的な目的から、基礎語彙表をつくっておられる。したがって、ある語の形が、どのように変化したかを、しらべることが必要である。
これにたいし、私たちの目的は、２つの言語の間に、偶然以上の関係がみとめられるかどうかをさぐることである。したがって、あとからの借用語は、のぞくことがのぞましい。
また、表記法も、コンピュータに入れる都合なども考慮し、服部氏と私だちとでは、若干異なるところがある。たとえば、服部氏「'juki （雪）」→安本「'yuki」、服部氏「cuci （地、上）」→安本「tsutʃi」（これは、「つ」の子音と「ち」の子音とを区別するため）など。さらに、東京方言のアクセントは、金田一京助監修『明解国語辞典』（三省堂刊）によってチェックした。

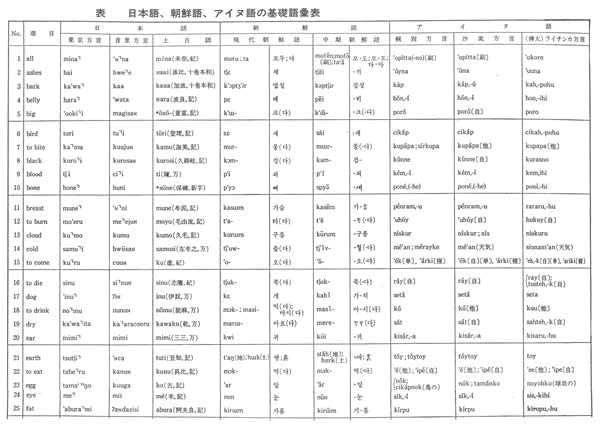
日本語、朝鮮語、アイヌ語の基礎語彙表を下記に示す。
（下図はクリックすると大きくなります）

■朝鮮語とアイヌ語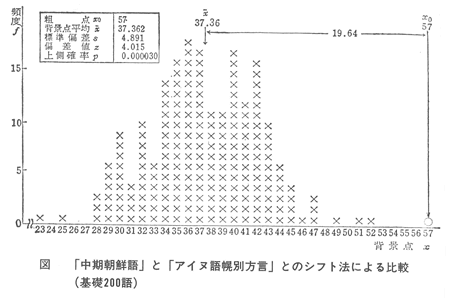
中期朝鮮語」と「アイヌ語幌別方言」とをとりあげ、「第１番目の子音検定法」によって、「シフト法」を行なう。
実際に行なった結果は、つぎのとおりである。
（１）「中期朝鮮語」と「アイヌ語幌別方言」とのばあい、第１番目の子音の一致数は、200単語中の57単語であった。すなわち、粗点ｘ0は、57である。

（２）199個の偶然による一致数、すなわち、背景点ｘを求め。その度数分布を、グラフに示せば、図のようになる。図には、粗点なども、あわせて記しておいた。

（３）背景点の平均値ｘは、37.362である。

（４）背景点の標準偏差sは、4.891である。

（５）偏差値を求めれば。
　　　　　 ｚ＝（57-37.362）／4.891＝4.015
で、4.015である。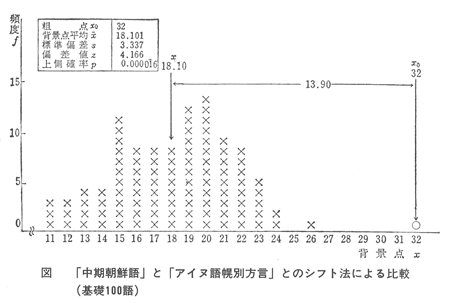

（６）この値以上の偏差値がえられる確率を求めれば、0.000030となる。すなわち、「中期朝鮮語」と「アイヌ語幌別方言」とのあいだにみられるような一致が、偶然によってえられる確率は、0.000030である。約十万回に三回程度しかおきない、まれなことである。それは、十円をなげて、十五回つづけて表を出寸確率にほぼ等しい。

このようなことがおきる確率は、かなりゼロに近いといってよいであろう。すでにのべたように、統計学では、ふつう、確率0.01（百回に一回）、または、確率0.05（百回に五回）を基準とし、この確率以下のばあいは、偶然以上の要因がはたらいているとみなす約束にしている。
「中期朝鮮語」と「アイヌ語幌別方言」との一致は、偶然以上の一致であるといえる。それは、ふつうの統計学の基準よりも、はるかに厳しい基準をもうけても主張できることである。

以上は、基礎二百語についてしらべた結果であるが、基礎百語について同様にして、「シフト法」を行なえば、図のようになる。やはり、「中期朝鮮語」と「アイヌ語幌別方言」とのあいだにみられるような一致以上の一致が、偶然によってえられる確率は、ゼロに近い。一致が偶然によってえられる確率は、0.000016で、約十万回に二回程度しかおきないことである。

■とりあげた四十八言語
私は、日本語と日本のまわりの計四十八の言語（おもに、東ユーラシア大陸の諸言語と太平洋上の島々の諸言語）をとりあげ、「シフト法」によって、語彙の近さの度合いをはかった。他に、日本語と印欧諸語との語彙の近さの度合いを、簡便法によってはかっている。
「シンフト法」によって調べた言語は、つぎの四十八言語である。これらの言語については、多数の言語学者の力ぞえをえて、まず、基礎語彙を作成した。これらの諸言語の使用人口の総数は、十五億人ないし二十億人と考えられる。とりあげた諸言語を地図上に記せば、下図のようになる。東のポリネシアから、西のハンガリー、フィンランドまで、日本を中心に、地球をおよそ半周する。

これら四十八言語の、２００語からなる基礎語彙表と、お力ぞえをいただいた言語学者のお名前は、拙著『日本語の誕生』（大修館書店刊）にのせている。「シフト法」は、第１番目の子音の一致をしらべる「語頭音検定法」によって行った。

 

四十八の言語の地域の地図を下記に示す。
（下図はクリックすると大きくなります）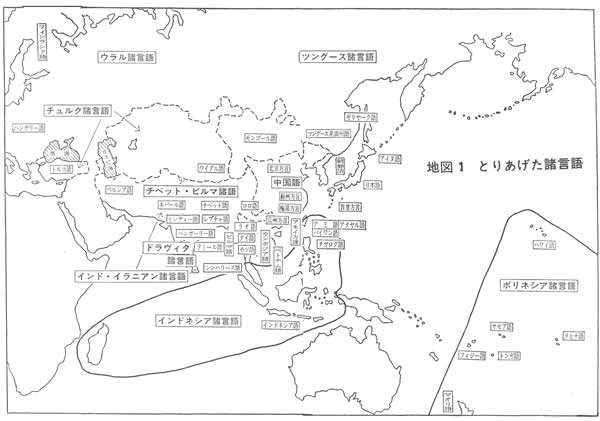

・アウストロネシア諸言語で一致が偶然によって得られる確率
（下図はクリックすると大きくなります）

 

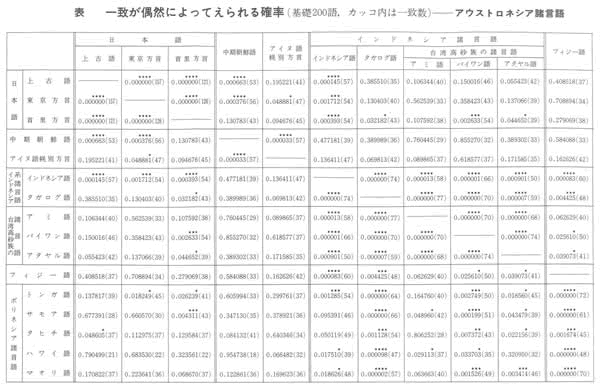
・上古語と一致する言語は、当然東京方言や首里方言は高い。中期朝鮮語より、インドネシア語や、カンボジア語の方が高い。
（下図はクリックすると大きくなります）

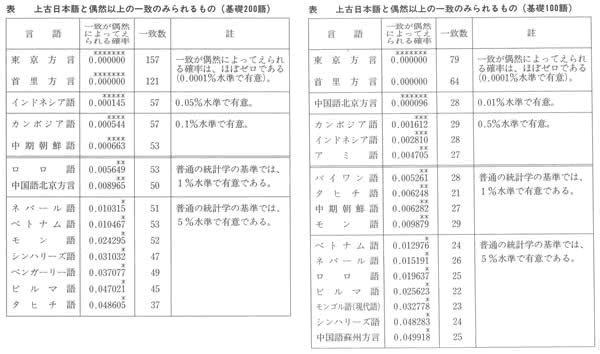
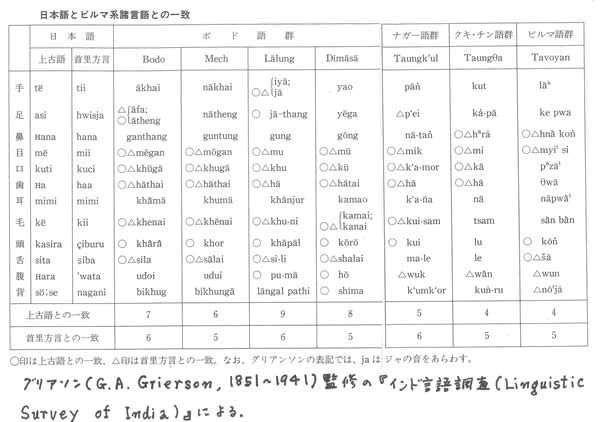
・英国がインドを植民地にしたころ、英国人のグリアソンがインド近辺の諸民族の言語を調査した。その調査結果が役に立っている。その中でビルマ奥地の諸言語が身体語について日本語に、ひどく近いことが分かった。ビルマ系諸言語（ナガ語、ボド語、ディマーサ語など）が行われている地域は下の地図にあるビルマ（ミャンマー）の奥地である。

・基礎身体語について、英語とドイツ語が一致するのと同じくらいに、上古日本語とポド語などは一致する。
（下図はクリックすると大きくなります）

・基礎身体語について、日本語と中期朝鮮語、アイヌ語、インドネシア語との一致をみると、中期朝鮮語、アイヌ語よりインドネシア語の方が多い。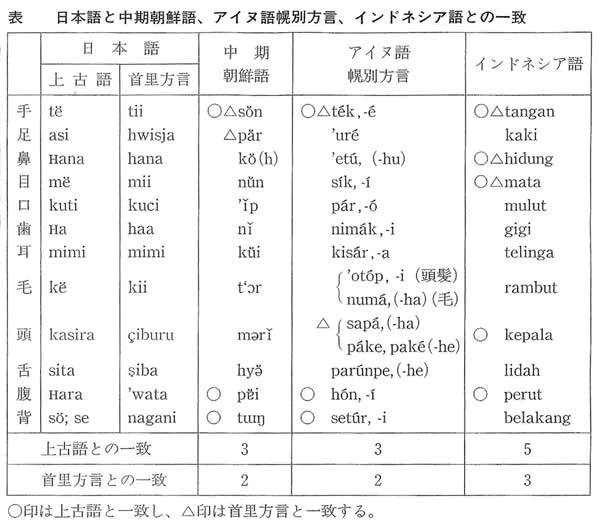

 

■言語の成立
（１）ピジン（pidgin）語
ピジンには、「商売」「取引」「仕事」などの意味がある。英語のbusiness（ビジネス）の中国なまりから来たという説もある。
ピジン語は、共通の言語をもたない複数の集団が接触して形成された言語の一種である。集団間コミュニケーションの必要性から、応急手段として形成される。
音声面では一方の言語の形を、単語と文法の面では他の言語の形を強く残したりする。文法は、かなり簡略化される。
ピジン語の話し手は、日常生活での母語を、かならず持つ。
ピジン語は、世界各地で多数みられる。太平洋諸島でのピジン英語は、よく知られている。

（２）クレオール（creole）語
二つ以上の言語が接触して、ピジン語が形成されたのちに、そのピジン語が、使用地域の人々にとっての、母語になってしまったばあいの言語を、「クレオール語」という。
カリブ海域のハイチ語、インド洋のセイシェル語、西アフリカのシェラーレオネのクリオ語などが、とくによく知られている。
典型的には、ピジン語使用者たちの子どもたちが、ピジン語を常用する人々となることによって、クレオール語が成立する。

クレオール語は、合理的に発達した文法と、ゆたかな語彙をもちうる。日常生活のあらゆる場面での使用に耐える。
発生してから時間がたつにつれ、そのクレオール語の構造のなかに、さまざまな不規則性なども発生し、やがては、通常の自然言語（natural language）と区別がつかなくなる。このことは、現在では、「通常の自然言語」とみなされている数多くの言語のなかに、じつは、クレオール起源のものが含まれている可能性を示唆する。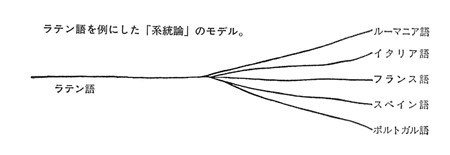

たとえば現在のスペイン語、フランス語、イタリア語、ポルトガル語、ルーマニア語などは、いずれも古代ローマで使われたラテン語から分裂し、独自に発達してきたものである。この場合のラテン語のように起源になった言語を「祖語」という。そして同一の祖語から分かれた言語を「同系語」、あるいは「２つの言語は系統が同じ」という。

このような「系統論」は、１つの祖語から多くの言語が分かれて出ることを想定している。すなわち、１つの源から出た流れが、多くの支流に分かれていくモデルである。印欧語のように、歴史上ほとんど常に他の言語に対して文化的に優位性をもち、ある源からあふれ出る形で発展してきた言語について、最もよく成立するモデルといえる。

しかし、日本語は全く逆に、多くの言語が流れ込む形で成立したと見なさなければならない。これは、多くの川が注ぎ込んで大河となるように、水源は１つとは限らないとするモデルである。このモデルのほうが、日本の地理的位置から考えても、歴史時代に入ってからもわが国に多くの異質の文化が流れ込んだことを考えても、自然であると思える。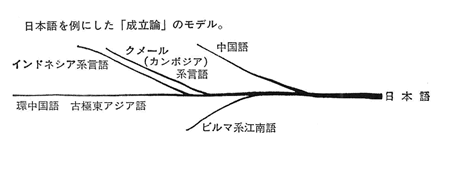

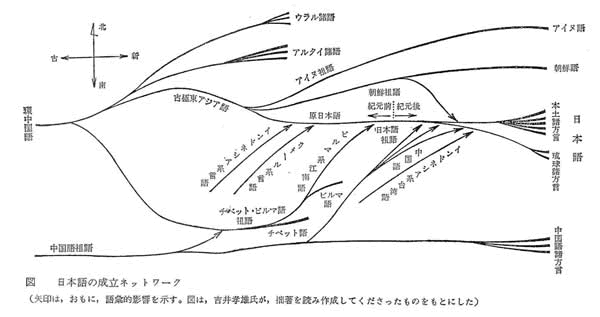
自然、という以上に、このようなモデルを考えないことには、日本語がいくつかの異質の言語と、統計的に偶然以上の一致を示す理由が説明できない。日本語と偶然以上の一致を示す言語をもとにつくった日本語成立についてのモデルが右図である。

結局、「日本語の起源」において成り立つのは、「系統論」ではなく、どのような言語が流れ込んだかの「流入論」、または、いかにして日本語が成立したかの「成立論」であると思われる。すなわち、日本語の成立に当たって流れこんだ言語としてどのようなものが考えられるか、そしてそれらの言語が日本語の成立にどう寄与したか、ということである。
印欧語は、ある源からあふれ出る形で発展したが、日本語は多くの言語が注ぎ込む形で成立している。この違いが、異なる形のモデルを要求するのである。

東京大学の教授であったすぐれた国語学者、時枝誠記（ときえだもとき）［1900～1967］は、『国語学原論続篇』（岩波書店、1955年刊）のなかで、私と同じようなモデルを、すでに五〇年以上まえに示している。
時枝誠記は、私がかかげたのと、きわめてよく似た図を示してのべる（要約）。
「人間の文化の歴史は、たえず異質的なものが、流れこんで、一つの新しい文化を形成して行くのが普通である。歴史的研究は、全体を、組成する要素に分析し、その全休が形成される経路を明らかにするところに使命があると見るべきである。一般に、文化史は、そのように記述されている。言語史も、例外ではないはずであるのに、ふしぎに、それらとは、揆（き）を異にしていた。言語は、文化のにない手であると言われている。文化が混淆すれば、言語が混淆するのは、当然である。

これまでの言語史研究は、その淵源である印欧比較言語学の性格に規定されている。そこでは、言語を、根源へ根源へさかのぼって、失われた祖語の再建に、学者の興味と関心が向けられた。そのさい、国語の中に流れこんだ異質物は、問題でなく、むしろ、それらを拭（ぬぐ）いさって、ただ源流を探ることが大切であった。

自然発生史の樹幹図にならって、言語発達史の樹幹図が作られるようになった。
従来の国語史研究による国語の位置づけを、樹幹図式に表わせば、右図のようになる。

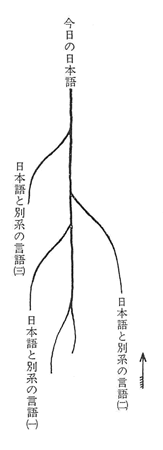
国語史は、国語を、その根源よりの分化発展として、樹幹図式に捉えるべきではなく、異分子の総合として、河川図式に捉えるべきである。
本書で考えられている国語史を図に表わせば、左図式に表わされることになるであろう。

一本の川には、水源を異にした大小幾多の支流が流れこんで、下流の大をなしている。それらの構成分子を分析し、それがどのように組みあわされて、下流をなしているかを明らかにすることが必要である。
日本の文化は、外来文化の絶えざる波状的な進入によって、古い文化の残存の上に、新しい文化が積み重ねられて、ここに文化の重層性ということが起こってきた。
国語も、古い文化圏の言語の上に、新しい文化圏の言語が重ねられるということが繰りかえされてきた。
古来、国語の中に流れ入った外国語は、日本周辺の言語としては、アイヌ語、朝鮮語、南方語、そして、最も徹底的には、漢語であり、また、漢語を媒介とする印度の古語梵語である。近世以後においては、ヨーロッパ諸言語がある。」

 

 

 

■日本語の成り立ち
要するに、日本語と朝鮮語とは関係が無くて、朝鮮語とアイヌ語の方が関係があるということになる。そうすると朝鮮語とアイヌ語とがある種のグループをなしていてそれがもともとの縄文語にあたるのではないか［古極東アジア語］。（下の右図）

そこに弥生時代に稲作と同時に戦乱を避けて、江南の方からビルマ系の言語が日本と朝鮮の南の方へ来た。またインドネシア系言語が海流に乗って、同じように日本と朝鮮の南の方へ来た。それが混じってピジン語からクレオール語をなすようになった。（下の左図）
（下図はクリックすると大きくなります）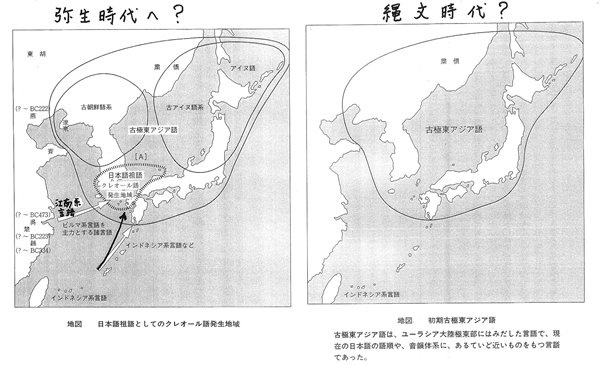

そのクレオール語が広がった、それが各地域的に発展して古代では、日本語系言語、アイヌ語系言語、朝鮮系言語と個別の言語系を構成するようになる。（下の右図）
現代は日本列島全体に日本語系が占めるようになった。（下の左図）
（下図はクリックすると大きくなります）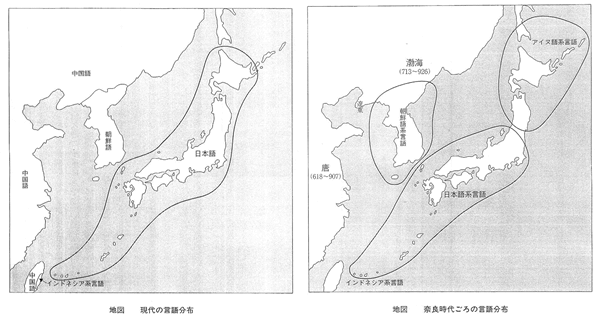

 

■「言語年代学」
「言語年代学」は、同じ祖語（祖先となる言語）から分かれた二つの言語が、今からおよそ何千何百年まえごろに分裂したのか、その年代を推定しようとする。

「言語年代学」の考え方そのものを理解するのには、数学についての知識を、若干必要とする。しかし、言語年代学の目的や成果を知りたいのであれば、数式計算をする必要はない。数学がわからなくてもよい。コンピュータも、もちろん使わなくてよい。グラフをみれば、そのねらいを、簡単に知ることができる。「言語年代学」の発想はおもしろい。日本語の起源の探究にも、参考となる多くの知見をもたらした。言語年代学の結果を、たんに、「『日本語と朝鮮語』が、かりに同系であるとしても、その分裂年代は『ドイツ語とフランス語』との分裂年代よりは古い。」
というような相対的な年代比較を行なったものとして読みとるていどならば、現在の言語年代学でも、十分有用である。

言語年代学は、1950年代に、アメリカの言語学者、スワデシュ（M.Swadesh）が、考案した。それは、考古学の分野で用いられる放射性炭素（炭素14）を測定して、遺物の年代を推定する方法にヒントを得たものであった。

いま、同一の祖語から分裂した二つの言語を考えてみよう。いま、なんらかの方法によって、その二つの言語間の近さの度合をはかってみる。もし、その二つの言語がきわめて近ければ、その二つの言語は、比較的現在に近い時期に分裂したことが考えられる。逆に、その二つの言語があまり近くなければ、その二つの言語は、古い時代に分裂したことが考えられる。すなわち、分裂してから時間がたてばたつほど、二つの言語は、へだたって行くことが考えられる。
言語年代学は、二つの言語間の近さをはかり、それによって、二つの言語が分裂した時期を推定しようとするものである。それは、換算によって、言語間の近さの度合を、時間軸上に投影しようとするものであるといえる。

・言語年代学グラフ（インド・ヨーロッパ諸語を基準とする分裂年代推定グラフ）
（下図はクリックすると大きくなります）

 

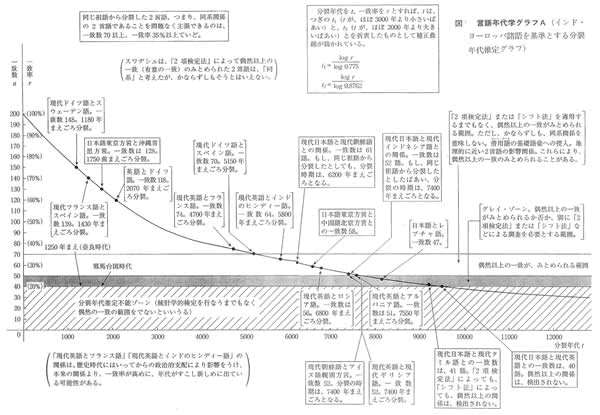
いま、ある祖語Ｐがあったとする。この言語を使っている民族が、いま、たとえば、Ａ、Ｂの二つの島に分かれて住んだとする。そして、それぞれの島で、それぞれの言語Ａ、Ｂを、独立に発展させて行ったとする。その結果、何千年かのちには、かなり異なった言語になったとする。基礎語彙（２００語または１００語）について考えてみる。言語Ａは、最初は、祖語Ｐと同じ基礎語彙をもっている。分裂してから１０００年後には、かりに、その基礎語彙のうちの２０パーセントが、ほかのことばにとってかわられ、８０パーセントだけが、もとのまま残ったものとする。

さて、この１０００年あたりの基礎語彙の残存率０．８が、つぎの１０００年にも、つぎのつぎの１０００年にも、つねにほぼ一定であるという仮定がなりたつものとしてみよう。すると２０００年後には、もとの基礎語彙の０．８の０．８、すなわち0.8↑2（＝６４パーセント）が残存することになる。３０００年後には、もとの基礎語粟の、６４パーセントの８０パーセント、すなわち0.8↑3（＝51.2パーセント）が、残存することになる。

言語Ｂにおいても、同じことがおきたとする。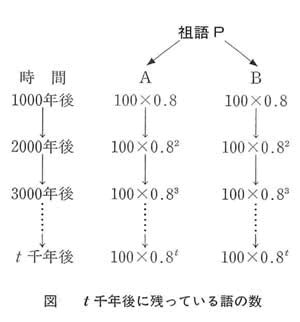

１０００年あたりの基礎語彙の残存率は、言語Ａとおなじく０．８であったとする。

一般に、ｔ千年後には、もとの基礎語彙の0.8↑tが残存することになる。

・日本語の起源の問題は、日本民族の起源の問題と密接に関係している。中国南方方面の言語文化の影響を無視できない。

・特定の「言語Ａ」（たとえば、レプチャ語、タミル語、朝鮮語）だけをとりあげて、日本語の起源の問題を説明する方法によるのは、方法的に問題がある。その言語Ａよりも、もっと日本語に近い言語が存在していないことが、証明されていない。
「言語Ａ」を選んだ段階で、「言語Ａと日本語とは関係があるはずだ」という人間の「判断」がはいっているのである。そのような「判断」がはいるのを、のぞくには、どうすればよいか。
日本語との近さの度合いを、一定の基準で、客観的に測定する。近さの度合を世界の多くの言語について、洗いざらいしらべる。現代は網羅的にビッグデータを処理できる時代になっている。
日本語と「偶然以上の一致（有意の一致）」のみられる言語を、とりだしていけばよい。・・・・・勝率の高い手をとる。

・問題を解決するとは、・・・・？　（日本語の起源や邪馬台国問題は碁や将棋より構造が単純な問題？）
（１）「評価」の方法をみつけること。日本語と偶然以上の一致を示す言語をみつけること。邪馬台国が存在する確率の大きい県をみつけること。
（２）「計算」の方法をみつけること。フィッシャー流の統計学、ベイズの統計学など。

・AIのプログラムを作る人は、碁や将棋の名人以上の実力をもつ人ではない。与えられた道具や技術を使いこなす人である。
コンピュータは、計算が速いが、プログラマーは、計算が速いわけではない。
「エミュレート」・・・主観や価値判断を加えずに、物事を判断すること。

今後の問題
・未調査の言語を調査する。ボト語、ナガ語、チュクチ語など。

・基礎語彙などの調査項目をふやす。拙著『言語の科学』では「基礎五百語」を選定している。

・検定法じたいの検討。「シフト法」「二項検定法」「一般シフト法」（吉田知行氏）など。結果はどの方法を用いても、それほど大きくは変わらない。（ブートストラップ法［bootstrap method、編み上げ靴のつまみ革法。再標本化法（りサンプリング）など。］

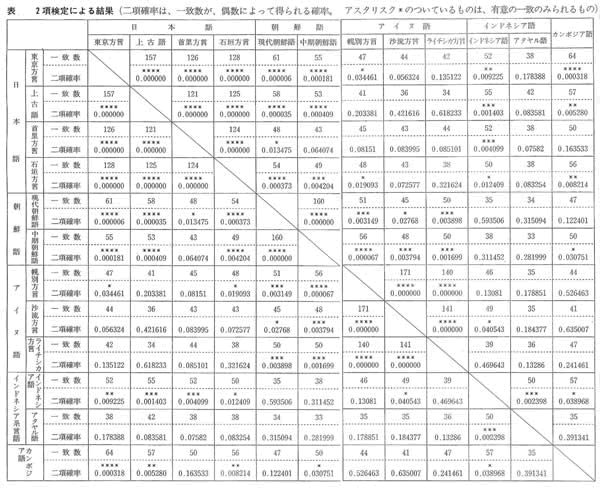
２項検定法の結果は下表である。
（下図はクリックすると大きくなります）

 

・日本語の成立について、分裂と流入をまとめると下図のようになる。
（下図はクリックすると大きくなります）

 

■日本語に関する拙著の紹介
（１）『日本語の誕生』（1978年、大修館書店刊）
コンピュータ・サイエンス専攻の産業能率大学教授、本多正久氏と共著。おもに東アジアを中心とする四十八言語の「基礎２００語」の原データがおさめられている。また、コンピュータで打ちだした諸言語間の一致が、偶然によって得られる確率（有意性の検定結果）の表など、算出結果データをかなりおさめている。1990年に、同じ出版社から、本書の新装版が出ている。

（２）『因子分析法』（1981年、培風館刊）
数学者、赤摂也氏監修の「現代数学レクチャーズ」のなかの一冊。（1）と同じく、本多正久凡と　共著。諸言語の分類技法などについて、その基礎や応用例を述べた本。

（３）『言語の科学』（1976年、朝倉書店刊）文部省統計数理研究所の所長であった統計学者、林知己夫（はやしちきお）氏の監修になる「行動計量学シリーズ」のなかの一冊。おもに、計量比較言語学の方法と応用例とをくわしくのべたもの。

（４）『言語の数理』（1976年、筑摩書房刊）
東京大学の助教授、国際基督（キリスト）教大学の教授、山梨大学の教授などをされ、現在大妻女子大学教授の数学者、野崎昭弘氏（中公新書のベストセラー『詭弁論理学』の著者）との共著。計量比較言語学の方法と応用例とをのべる。（3）の『言語の科学』は、（4）の『言語の数理』の安本執筆の部分をもとに、加筆、改訂したもの。

（５）「日本語の成立」（1978年、講談社現代新書）
「計量比較言語学」の方法と成果とを、一般むきにまとめたもの。

（６）『日本語の起源を探る』（1985年、ＰＨＰ研究所刊、新書版）
一般むきの本である。（5）にくらべ、細部についての検証を加えている。

（７）『日本語の起源を探る』（1990年、徳同文庫）
（6）を、文章化したもの。

（８）『朝鮮語で「万葉集」は解読できない』1990年、ＪＩＣＣ（ジック）出版局［現、玉島社］刊）
『万葉集』を、朝鮮語で解読したとするベストセラー本が、たんなるコジツケ集にすぎないことをのべたもの。

（９）『新・朝鮮語で万葉集は解読できない』（1991年、ＪＩＣＣ（ジック）出版局［現、玉島社］刊）
（8）を増補したもの。データや理論的根拠などを、さらに書き加えた。

（１０）『日本語はどのようにつくられたか』（1986年、福武書店刊）
「日本語の起源」について、小中学生、高校生むきの読物風にまとめたもの。図版や写真などが多い。

（１１）『日本人と日本語の起源』（1991年、毎日新聞社刊）
日本語の起源について得られた結果などもとりいれ、日本人の起源について考えた本。

（１２）『新説！日本人と日本語の起源』（2000年、宝島社刊）
（11）の本に、さらに新しい情報、データをおぎなったもの。ただし、旧石器捏造事件発覚前に刊行された本であるため、旧石器時代にふれた箇所では、一部誤った情報を含む。

（１３）『倭人語の解読』（2003年。勉絨出版刊）
このシリーズの一冊。『魏志倭人伝』中にみられる「倭人語」をとりあげ、それが、のちの「日本語」と、どのように結びつくかを考察したもの。

以上のほか、1972年2月号から、八回にわたって、『数理科学』（ダイヤモンド社刊）に連載した「日本語の誕生」、1977年1月号から十二回にわたって『言語』（大修館書店刊）に連載した「日本語の起源を探る」には、単行本におさめられていないデータなどが載せられている。