新たに日本の通史を始める。
まず「日本民族の起源」について、

■民族と人種と国民
・民族（広辞苑より）
文化の伝統を共有することによって歴史的に形成され、同属意識をもつ人々の集団。文化の中でも特に言語を共有することが重要視され、また宗教や生業形態が民族的な伝統となることも多い。社会生活の基本的な構成単位であるが、一定の地域内に住むとは限らず、複数の民族が共存する社会も多い。また、人種・国民の範囲とも必ずしも一致しない。

・人種
人間の生物学的な特徴による区分単位。皮膚の色を始め頭髪・身長・頭の形・血液型などの形質を総合して分類される。最近は遺伝子による分析が行われるがこれは人種の概念が強い。
①コーカソイド（類白色人種群）
②モンゴロイド（類黄色人種群）
③ネグロイド（類黒色人種群）
の三大人種群に分類されるが、下記２人種も加え、５大分類も行われている。

④オーストラロイド（類オアーストラリア人種群）
⑤カボイド（コイサン人種群）
　　 コイ族：アフリカ南西部で俗称ホッテントット、
　　 サン族：アフリカのカラハリ砂漠を中心にアンゴラから南アフリカにかけて住む、
　　 俗称ブッシュマン

・国民（広辞苑より）
国家の統治権の下にある人民。国家を構成する人間。国籍を保有する者。国権に服する地位では国民、国政にあずかる地位では公民または市民と呼ばれる。

日本人の起源について、いろいろな本が出ているが、遺伝子的関係の本が多い、日本人がどうかについて遺伝子関係で調べると、次の問題がある。

例として、アメリカについて、今から２０００年を経て、アメリカ人とは何かということを遺伝子学的分析をすると、白人、黒人、黄色人種、アメリカインディアンの要素が出てくる。しかし、言語を調べると２０００年を経ても英語系であろうと証明できる。ヨーロッパ系の言語となる。要するに、遺伝子の分析と言語の分析では明らかに異なる。

日本人ついて、遺伝子で分析すると、北のシベリヤからやって来たらしい、中国の北からもやって来たらしい、中国の南からもやって来たらしい、マレーシア、ポリネシアからもやって来たらしいとなる。しかし日本人はどこからやって来たかの明確な回答にならない。遺伝子分析は１万年位の長い昔には有効であるが、２０００年くらいの単位の場合は言語とか、風習とかの文化的な面の分析の方が日本人の起源の回答が求めやすい。

■倭人の家
中国雲南省晋寧と石寨山（せきさいざん）と日本の弥生時代ごろの共通性には鵜飼、家の建築様式、弓の形状（人の身長より長い弓）などの共通性がある。日本の福岡県の志賀島から出土した金印に似た蛇の図柄の付いた印が出ている。

 

その中で、今日は第一回として「倭人の家」について話す。

中国の雲南青銅器の写真がある。

 

これらの家の形は、日本の銅鐸に書かれている家や埴輪の家と同じような干欄（かんらん）式建築である。これは高床式建築の一つで、中国の揚子江流域にあるものである。特徴は屋の上部が長く、下部が短い。千木、鰹木がある。

日本の古代の干欄式建築。

 

上図から日本の古代の家と共通であることが分かる。

千木が発達させるのは、現代でも雲南の哈尼（はに）族の家やインド東北部、アッサム地方の家のようにやたら千木が大きい家がある。日本でも継体天皇陵と思われる今城塚古墳から出土した大きな家の埴輪（高さ１７０センチ）など千木がやたらに大きい。

何故、屋根の形が逆さ台形かというと、高床の家は稲作地帯であるので、湿地帯で雨が多い。そこで、雨が降り込まないようにするため突き出ている。

雲南省石寨山との文化の共通性として、言語においても、ロロ語は子音が先頭に来る単語（コンソナントクラスタ）ではないこと、主語、述語、目的語の順番が日本語と同じなど共通性が高い。ポリネシアの言語も同じである。

今のベトナムの林邑（りんゆう）で、高床式住宅であると伝えられている。

 

中国の戦国時代（BC403～BC221）に中国の南の地域に楚の国があった。楚の国の地図参照。

・司馬遷の『史記』の「西南奥列伝」から
「はじめ、楚の威王のときに、将軍荘蹻（そうきゃく）に命じて、兵をひきいて長江の流れに沿ってのぼり、巴郡（はぐん）［現在の四川省重慶のあたり］・黔中（けんちゅう）［地図参照］以西を攻略させた。荘蹻は、もとの楚の荘王（そうおう）の後裔であった。荘蹻は、滇池（てんち）［前の地図2参照］にいたった。滇池の広さは方三百里。付近一帯の平地は、数千里におよんでよく肥えていた。兵の威力でこれを平定し、楚の属地とした。帰って報告をしようとしたところ、たまたま秦が楚の巴郡・黔中郡を攻略したために、道がふさがり、通ることができなくなった。よって荘蹻は引きかえし、部下を引きつれて、滇の地の王となった。その土地の風俗にしたがって、服装をかえ、その地の長となった。」荘蹻が滇の地にはいった年代は、『後漢書』の「西南夷伝」では、楚の頃襄王（けいじょうおう）［紀元前２７７～紀元前２６３］の時代としている。荘蹻が滇の地で王になって以後、その子孫が王位を伝え、数百年つづいた。」
とある。

秦の始皇帝が楚の国を滅ぼした。その結果楚の国人々が避難したり逃げたりして、その文化が、雲南やベトナムや日本へ広がったのではないか。

昨年１０月に「探究の基礎構造」を講演した時に、講演が途中で終わったので、今回はその続きを話す。
■１０月の講演
・認識論
・科学とは何か
・「数字」や「数学」で表現する意味
・正確な地図
・事実による説得
・演繹型と帰納型
・前提の設定

１０月の講演の続きとして、
■パスカルとヒルベルト
フランスのパスカルは、演鐸型の論理をとりあげている。パスカルは、すでに１７世紀に、その著『幾何学的精神』の第二部「説得術について」という文章のなかで、論理による説得、あるいは論証の基本的な方法などについて、明快に説明している（吉田洋一・赤摂也共著『数学序説』［培風館刊］参照）。

パスカルは、まず、「定義」について、次の三つの規則をあげている。
①それよりもはっきりした用語がないくらいあきらかなものは、それを定義しようとしないこと。（すべての言葉を定義するのは不可能なため。）
②いくぶんでも不明、もしくはあいまいなところのある用語は、それを定義しないままにしておかないこと。
③用語を定義するにさいしては、完全に知られているか、または、すでに説明されていることばのみを用いること。

　次に、パスカルは、「公理」について、二つの規則をあげている。公理というのは、議論の出発点、または前提ともいわれるものである。
①必要な原理は、それがいかに明晰（めいせき）で、明証的－－つまり一見してだれでもが納得できるような形であっても、けっして、承認されるか否かを吟味（ぎんみ）しないままに残さないこと。
②それ白身で完全に明証的なことがらのみを、公理として要請すること。

さらにパスカルは、「論理」について、三つの規則をあげている。
①それを証明するために、より明晰なものを探してもムダであるほど、それだけで明証的であることがらは、これを論証しようとしないこと。
②少しでも不明なところのある命題は、これをことごとく証明すること。そして、その証明にあたっては、きわめて明証的な公理、またはすでに承認されたか、あるいは証明された命題のみを用いること。
③定義によって限定された用語のあいまいさによって誤らないために、つねに心のなかに、定義された名辞の代わりに、定義をおきかえてみること。

以上のパスカルの方法をまとめてみると、「自明のものをのぞく、すべてのことばを定義し、また自明でないすべての命題を証明しつくす」ということになる。
　 このパスカルの論証の方法というのは、ギリシア人が幾何学を築くのに用いた方法にほかならない。すなわち、ある「公理（前提）」といったものを設定しておいて、そこからひじょうに多くの「定理」といったものを導きだす、という方法である。きちんと決めた前提から、さまざまなものを、正しい論理に従って導きだす、ということである。だからこそパスカルは、自分の書物を『幾何学的精神』と名づけた。

　ところで、以上のような方法論は、１９世紀以来の自然科学のめざましい発展とともにさらに洗練されてきている。「幾何学的精神」の代表的な形としては、「公理主義」といわれるものがある。ある理論において、ほかの命題の前提となる基本的な命題の体系－－これを公理系という－－をあきらかにし、その公理系と、特定の推論規則から演鐸的に理論をくみたてることを、公理論的方法または公理論と呼ぶ。ユークリッド幾何学は、不完全なものであっても、その適切な例であるといえる。また、すでに述べたパスカルの方法は、公理主義の原初的な形といえる。
　 現在の公理主義が、パスカルの説いた方法と根本的に異なる点は、主として公理というものについての考え方にある。パスカルにおいては、公理というのはそれ自身、完全に明証的なことがらで、すべての人に承認される明晰なことがらでなければならない、と考えられた。
　 ところが１９世紀のはじめに、万人に承認されたとはいえない公理をもとに、完全に矛盾のない非ユークリッド幾何学（リーマン幾何学など）が建設された。このために、パスカルが述べたような意味での公理に対する考え方が、大きくゆらいだ。そして、ドイツの大数学者、ダヒト・ヒルベルト（１８６２～１９４３）によって、公理の考え方についての大転換が行われた。

　一言でいえば、ヒルベルトは、公理は、なんら自明の真理である必要はなく、たんに、明確に定められた仮定で十分である、としたのである。すなわち、いくつかの仮定をおき、そこから形式的に結論を導いて、そこに矛盾を生じなければよい、としたのである。ヒルベルトは数学の基礎として、自分の考えを述べた。しかし、その考え方は、やがて自然科学全体に、そして社会科学の分野にも、きわめて広範な影響をおよぼすことになった。
　 オーストリアに生まれ、のちアメリカに渡った、物理学者で科学哲学者、ルドルフ・カルナップ（１８９１～１９７０）らは、この方法（公理的方法）だけが科学的方法であり、すべての科学は公理論的に構成されるべきであるとして、公理主義をとなえた。さらにカルナップらは、それまで主として、数学を基礎づける道具として発達してきた記号論理学を、広く諸科学を分析し、基礎づける道具として用いることを主張した。西欧の現代哲学である分析哲学では、公理主義が深く根を下ろしている。

一つの例をあげよう。
　 太陽と地球との関係について、地動説と天動説と呼ばれるものがある。きわめて多くの人が自然に認めることがらに立脚すれば、天動説のほうに分かある。すなわち、太陽は東から昇って、西に沈む、というのは、私たちが直接目にする事実である。明証的な事実であるといえそうである・しかし、天動説のほうが正しいとはいえない。
　 地動説は、太陽は動かず、地球がそのまわりをまわっているのだと主張する。地動説のほうが正しい、ということになったのは、この立場に立ったとき、ひじょうに多くのことが、矛盾なく、うまく説明できるからである。すなわち、地動説の仮定に従ったほうが。多くの観測事実を、矛盾なく説明できるのである。

　いま一度まとめてみよう。
　 議論を行うばあい、パスカル的な方法は、だれもが認めることを前提として、議論を進めていき、だからこの結論は正しいのだということを、認めさせるやり方である。
　 これに対して、ヒルベルト的方法では、前提はだれもが認めるようなものでなくてもかまわない、ということになる。そして一応の「仮説」として、あることがらを前提にし、それによって多くのことがらが矛盾なく説明できれば、もとの仮説を正しいものとして受けいれよう、ということになる。

　私たちの日常生活においては、あるいは社会科学、人文科学などの分野においては、だれもが認める事実というものは案外少ない。けっきょく、「まあここらあたりが、だいたい正しいところかな」ということがらを前提にして、議論を展開しなければならないことが、しばしばある。

　パスカル的なやり方は、論証としてはスマートだが、柔軟さにおいては、ヒルベルト的方法のほうが、すぐれていることが多い。

 

■論理による説得の手つづき
　 論理による説得、論証による説得というのは、一般に若い人が得意とする説得の方法である。まず自明のように思われることを、相手に認めさせる、そして、相手がひとたびそれを認めればシメたものである。こうだからこうだ、だからこうだ、と論理を展開して結論を出し、それを相手に認めさせる。相手は前提を認めた以上、結論も認めざるをえない。
　 ところが、このような論理展開を行ったばあい、なるほど、理屈はそのとおりだ、しかし、結論がどこかおかしい、という疑問を抱かせることがしばしばある。西洋の中世のスコラ哲学（おもにキリスト教の教義を、アリストテレスの哲学などによって体系づけ、説明しょうとするもの）にしても天動説にしても、論理的にはきわめてととのったものだった。しかし、それは、対象を説明しうる唯一の説明体系ではなかった。対象をもっと適切に説明しうる体系が、ほかにあった。論理的にととのっているということだけでは、その説明体系がもっとも妥当なものであるという保証には、かならずしもならない。
　 論理による説得は、論理的にととのっていれば正しいという態度を、しばしば生みがちである。論理的に導きだした結果が、現実とよく合致しているかどうかを、もう一度よくチェックしてみる必要がある。そのチェックが落ちていると、論理的にはととのっているが、現実や事実と合わないというようなことが、しばしば起きる。「理路整然と間違っている」というようなことになるのである。
　 そのような問題はあるにしても、論理による方法は、ほかの方法にくらべて、きわめて体系的で、構造的な知識をもたらすことも事実である。
　 論理による説得を行うには、一般的に、どのようなことに気をつければよいのだろうか、
論理による説得は、次のような手つづきによって行われると考えられる。
①具体的な多くの事実やデータから、比較的わずかな、いくつかの前提（仮説、仮定）を導きだす（いわゆる「帰納」を行う）。
②そのいくつかの前提を出発点として、形式的にととのった、落ちのない議論を展開し、結論を導きだす（「演鐸」を行なう）。
③その結論を、具体的な事実やデータと、いま一度照らしあわせて、矛盾することがないかどうかを調べる（事実とつきあわす）。
④矛盾したぱあいは、いま一度前提を検討し、前提を修正するか、あるいは、ほかのもっと適切な前提を選ぶ。新たな前提によって、②以下の手つづきをくりかえす。
⑤このようにして、矛盾なく対象を説明する体系がえられたならば、他を説得しうるものとして、提示することができる。

　この流れを図に示せば、図のようになる。

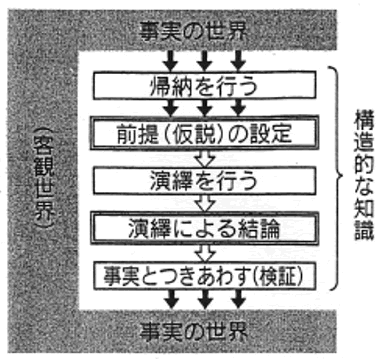
　論理による説得を行うばあいには、適切な前提を選ぶこと、結論を具体的世界の事実やデータと、いま一度照らしあわせて、矛盾がないかどうかをよく検討すること、などが大切である。

　政治的なある立場や、ある種のイデオロギーにもとづく議論などにおいて、途中の議論そのものはきわめて論理的なのだが、適切な前提が選ばれているかどうか、えられた結論が、現実の社会によく合致しているかどうかという検証が脱けおちていることがよくある。

 

■パラダイムの変換
すでに述べたように、現代の科学方法論では、議論の出発点となる仮説の任意性が主張
されている。
　 そのため、仮説の設定の仕方によって、ものの見え方、考え方が大きく変わってしまうことがある。
　 これを、「パラダイム・シフト」という。
例：図を見ると、若い女性に見えるし、お婆さんに見える。見方によって変わるのである。

　「中世のヨーロッパでは、太陽が地球のまわりをまわっているという天動説が、当時の宇宙論を支配していた。ところが、１６世紀にはいると、コペルニクスが、地球が太陽のまわりをまわっているという地動説を提唱する。このコペルニクスの地動説は、当時容易には受けいれられなかったが、一世紀にわたって議論が行われ、現在では、常識的な知識の一つとなっている。
　 そして、この転回に端を発して、科学的な概念の枠組みが大きく変わった。みえている世界や宇宙には、なんの変化もなかったが、われわれが宇宙をみるときの姿勢や考え方にとって、この転回はきわめて劇的なものであった。
　 このような新しい概念、パースペクティブの転換や創造を、科学者は、”バラダイム（新しい世界観）の創造”と呼んでいる。
　 この”パラダイム”いう言葉は、アメリカの科学史家であり、哲学者でもあるトーマ
　 ス・クーン（Thomas.S.Kuhn　１９２２～１９９６）が、１９６２年、その著書『科学革命の構造』（みすず書房刊）で、はじめて提唱したものだ。パラダイムは、ギリシア語で、パターンを意味する”バラディグマ”に由来しており、クーンは、これを特定の科学の基礎となっている支配的な論理的枠組み、あるいは、一連の仮説という意味で用いた。」

 

■学説の優劣を判断するための基準
①議論を行うための前提（公理、仮説）は、よく整理されているか。
例：私（安本）の仮説系
【前提１】
　 『古事記』『日本書紀』に記されている天照大御神以下の五代、および、歴代の天皇の存在。および、その順序は、一応信じられるものとする。すなわち、「代の数」は、信じられるものとする。
【前提２】
　 「父子継承」記事は、信頼できないものとする。そして、用明天皇以前においても、継承関係がほぼ確かな、用明天皇から桓武天皇におけると、あまり変わらない形で、継承がおこなわれたものとする。したがって、古い時代の諸天皇などのだいたいの活躍の時期は、活躍の時期がはっきりしている諸天皇の、一代平均の在位年数をもとに、推定しうるものとする。

②その理論はシンプルか。
例１：福永伸也（大阪大学）の『三角縁神獣鏡の研究』
福永氏は本のなかでも『三角縁神獣鏡の研究』複雑でむずかしと書いているが、その本は非常に複雑であり、分かりにくい。やはり理論はシンプルでなくてはいけない。

例２：村上斉（ひとし）『宇宙はなぜこんなにうまくできているのか』（集英社２０１２年）
「科学の理論はシンプルなほうがよい、という話をしました。その意味では、この統一も非常に重要です。さまざまな現象をいちいち別の理論で説明するのは、話が複雑になりますし、美しくもありません。ひとつの法則で多くのことを説明できたほうが、より深い原理に近づいたことになるでしょう。
　 そのため、大昔から現在にいたるまで、物理学者たちはさまざまな理論を統一する努力を続けてきました。物理学の歴史は統一理論の歴史だといっても過言ではありません。この世に起こるすべての現象をひとつのシンプルな理論で説明したい－－それが、私を含めた全世界の物理学者の夢なのです。ニュートンの万有引力の法則は、そんな統一理論の先駆けとなるものでした。」と書いている。

③その理論は統一理論化か。
議論で統一性がある方が優れている。邪馬台国論争を例にすれば、
例：私（安本）の理論
上記仮説前提から、第３１代の用明天皇から第５０代の桓武天皇までの天皇の１代の平均在位年数が10.88年となる。用明天皇からさかのぼり、神武天皇まで計算すると神武天皇は卑弥呼の年代に届かない。更に５代さかのぼり、天照大神とすると、卑弥呼の時代と合う。『古事記』『日本書紀』のなから、天照大神は九州に居たと考えられる。などと理論が展開でき、『魏志倭人伝』など中国、朝鮮文献、『古事記』『日本書紀』など日本文献、更に考古学的事実も調べその中で、矛盾がない理論となる。
例：畿内説の多くは
鏡だけを調べる、または土器だけを調べる。これではあぶない。

山片蟠桃の『夢之代（ゆめのしろ）』－－津田左右吉史観の先駆

　不合理な記述をふくむものは歴史を構成する史料としてみとめるべきではないと最初に強く主張したのは、江戸後期の大坂の町人学者、山片媛桃（１７４８～１８２１年）であった。
　 「蟠桃」は、「番頭」であった。倒産寸前となった主家升屋を、番頭として縦横の商才を発揮して大坂屈指の豪商に仕あげた鬼才であった。そしてまた、当時の、大坂第一流の町人学者であった。山片蟠桃の、生涯をあつかった小説に、南原幹雄著『伊達藩征服』（徳間文庫）がある。
　 今日でも、じつに多くの人々が、さまざまな人生航路のすえに、古代史の世界に深入りしていく。山片蟠桃も、また、そうであった。いつの時代でも、私たちは古代に思いをはせるとき、この世のさまざまな束縛や悩みから解放される。ひとときの心の自由を得ることができる。晩年の山片蟠桃は、失明と病苦とに悩まさていた。蟠桃は、死期の近づいてきたことを悟り、十数年のあいだ書きためていた原稿を、口述筆記によって補い、完成させる。『夢之代』と題する１２巻の大著を書き終えたのは、死の前年の１８２０（文致３）年のことであった。
　 孔子の弟子に、十哲の1人に数えられる宰我（さいが）がいた。宰我が昼寝をして叱られた話が『論語』にある。
　 『夢之代』は、宰我の昼寝の夢の代償という意味である。『夢之代』は、当時最新の、自然科学、社会科学、人文科学のすべてを論じ、そのうえに立って、蟠桃みずからの思想を述べたものであって、日本古代史のことだけを論じた書物ではない。しかし、古代史にもそうとうのページをついやしている。
　 「地獄なし極楽もなし我もなし、ただ有る物は人と万物」
　 「神仏（かみほとけ）化け物もなし、世の中に、奇妙不思議の事はなおなし。」
　 このように述べる蟠桃は、地獄も極楽も信じなかったし、また、神も神話も信じなかったのである。山片蟠桃は、商人的実証主義、唯物論的合理主義のうえに立っていた。山片蟠桃は、『夢之代』のなかでいう。
　 「日本紀神代の巻は取るべからず。
　　 日本の神代のことは、存して論ぜずして可なり（不合理な話がそこに存在しているままにして、議論しないのがよい）。」
　　 山片蜷桃は、日本の神話は作られたものであり、神武天皇から仲哀天皇までの記録も、歴史的事実としては信じられないことが多い、と説く。これは、のちの津田左右吉の学説にほぼそのままつながるものである。
　　 山片蟠桃はいう。
日本へ文字が渡ってきたのは応神天皇の時代であって、それからあとのことは、事実がはっきりしている。それ以前のことは、口で伝えた伝説であって、そこから事実をとりだすことはできない。
中国の三皇のこと、日本の神代のことは、そのままにして論じないでよい（存して論ぜずして可なり）。
　 『日本書紀』の神代の巻は、とるべきではない。神武以後も、それほど信頼できず、第１４代仲哀天皇、第１５代応神天皇の記事から歴史書として用いることができる。神功皇后の三韓退治の話は、妄説が多い。応神天皇からは、確実とすべきである。
　　 日本の国常立尊（くにとこたちのみこと）の話、中国の盤古（ばんこ）の話、インドの阿弥陀の話などは、みな作ったものである。そのままにして、論じないでよい（存して、論ぜざるべし）。
　 神武天皇から千年ほどのあいだは、神代の名ごりであって、『古事記』『日本書紀』をはじめとする史書にはどのように記載されていようと、みな作ったものである。もちろん、神代のことは、なおさら、夢のようなものである。」

山片蟠桃から津田左右吉へ
　 山片蟠桃のパラダイムをうけついだのが、津田左右吉（１８７３～１９６１年）である。津田左右吉は、第二次大戦のまえに、『神代史の新しい研究』（１９１３）、『古事記及び日本書紀の新研究』（１９１９）、『神代史の研究』（１９２４）など、一連の著述をあらわし、『古事記』『日本書紀』などの文献の史料としての価値について、くわしい研究を行った。
　 津田左右吉は、おもに、『古事記』『日本書紀』の記述のあいだのくいちがい、あるいは相互矛盾をとりあげヽそこから、『古事記』『日本書紀』に記されている神話は、天皇がわが国の統一君主となったのち、欽明天皇の時代のころ、すなわち、六世紀の中ごろ以後に、大和朝廷の有力者により、皇室が日本の統治するいわれを正当化しようとする政治的意図にしたがってつくりあげられたものである、と説いた。
　 端的にいえば、神話は、いわば机上でつくられた虚構であり、事実を記した歴史ではない。ただ、それをつくった古代人の精神や思想をうかがうものとしては、重要な意味をもつ、とする。
　 左翼思想・自由主義思想弾圧の時代にはいり、津田左右吉の研究は迫害される。昭和１５年、津田左右吉の著作は発売禁止の処分をうけ、ついで、津田自身が、皇室の尊厳を冒涜した疑いで起訴され、その学問的活動は封殺された。しかし、津田左右吉の所説は、第二次大戦後、はなばなしくよみがえる。津田左右吉の精神のやや否定的な傾向は、戦後の、すべて否定的、懐疑的となった風潮と合致し、大きく開花する。
　 井上光貞（１９１７～１９８３年）、家永三郎（１９１３～）、藤間生大（１９１３～）、水野祐（１９１８～２０００）、直木孝次郎（１９１９～）などの諸氏の研究は、津田左右吉の流れのうえに位置づけてよいであろう。最近、古代史についての論著をしばしば発表している松本清張も、この立場に近い。
　 今日、津田左右吉流の方法こそ唯一の、科学的・合理的方法であるように説く人がいる。
　 しかし、長い歴史のうえで眺めれば、津田左右吉流のパラダイムも、やはり、多くの古代史探究のパラダイムのなかの一つ、と考えるべきである。